On the Actionability of Outcome Prediction

Predicting future outcomes is a prevalent application of machine learning in social impact domains. Examples range from predicting student success in education to predicting disease risk in healthcare. Practitioners recognize that the ultimate goal is not just to predict but to act effectively. Increasing evidence suggests that relying on outcome predictions for downstream interventions may not have desired results. In most domains there exists a multitude of possible interventions for each individual, making the challenge of taking effective action more acute. Even when causal mechanisms connecting the individual's latent states to outcomes is well understood, in any given instance (a specific student or patient), practitioners still need to infer -- from budgeted measurements of latent states -- which of many possible interventions will be most effective for this individual. With this in mind, we ask: when are accurate predictors of outcomes helpful for identifying the most suitable intervention? Through a simple model encompassing actions, latent states, and measurements, we demonstrate that pure outcome prediction rarely results in the most effective policy for taking actions, even when combined with other measurements. We find that except in cases where there is a single decisive action for improving the outcome, outcome prediction never maximizes "action value", the utility of taking actions. Making measurements of actionable latent states, where specific actions lead to desired outcomes, considerably enhances the action value compared to outcome prediction, and the degree of improvement depends on action costs and the outcome model. This analysis emphasizes the need to go beyond generic outcome prediction in interventional settings by incorporating knowledge of plausible actions and latent states.

Lost in Translation: Reimagining the Machine Learning Life Cycle in Education

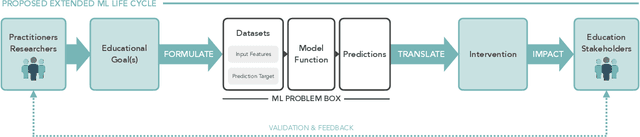
Machine learning (ML) techniques are increasingly prevalent in education, from their use in predicting student dropout, to assisting in university admissions, and facilitating the rise of MOOCs. Given the rapid growth of these novel uses, there is a pressing need to investigate how ML techniques support long-standing education principles and goals. In this work, we shed light on this complex landscape drawing on qualitative insights from interviews with education experts. These interviews comprise in-depth evaluations of ML for education (ML4Ed) papers published in preeminent applied ML conferences over the past decade. Our central research goal is to critically examine how the stated or implied education and societal objectives of these papers are aligned with the ML problems they tackle. That is, to what extent does the technical problem formulation, objectives, approach, and interpretation of results align with the education problem at hand. We find that a cross-disciplinary gap exists and is particularly salient in two parts of the ML life cycle: the formulation of an ML problem from education goals and the translation of predictions to interventions. We use these insights to propose an extended ML life cycle, which may also apply to the use of ML in other domains. Our work joins a growing number of meta-analytical studies across education and ML research, as well as critical analyses of the societal impact of ML. Specifically, it fills a gap between the prevailing technical understanding of machine learning and the perspective of education researchers working with students and in policy.

Strategic Ranking

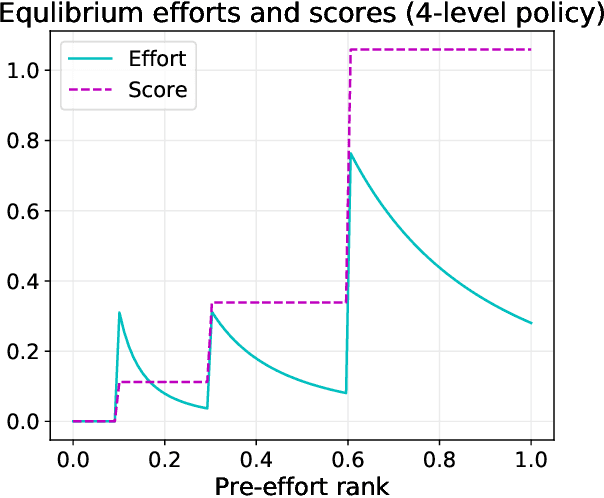
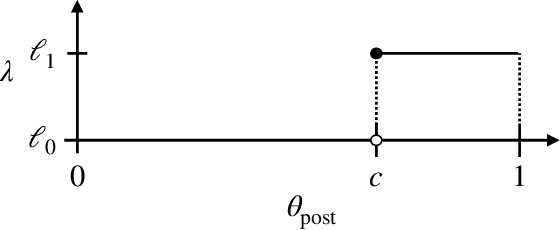
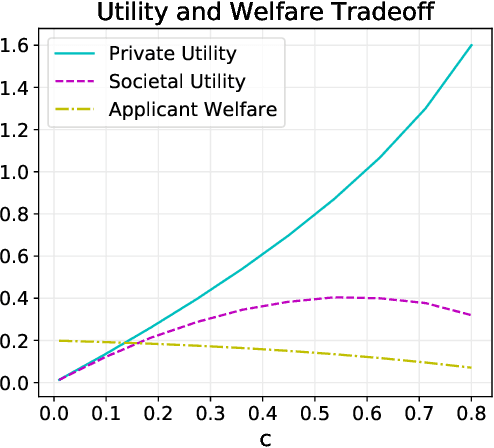
Strategic classification studies the design of a classifier robust to the manipulation of input by strategic individuals. However, the existing literature does not consider the effect of competition among individuals as induced by the algorithm design. Motivated by constrained allocation settings such as college admissions, we introduce strategic ranking, in which the (designed) individual reward depends on an applicant's post-effort rank in a measurement of interest. Our results illustrate how competition among applicants affects the resulting equilibria and model insights. We analyze how various ranking reward designs trade off applicant, school, and societal utility and in particular how ranking design can counter inequities arising from disparate access to resources to improve one's measured score: We find that randomization in the ranking reward design can mitigate two measures of disparate impact, welfare gap and access, whereas non-randomization may induce a high level of competition that systematically excludes a disadvantaged group.

Bandit Learning in Decentralized Matching Markets

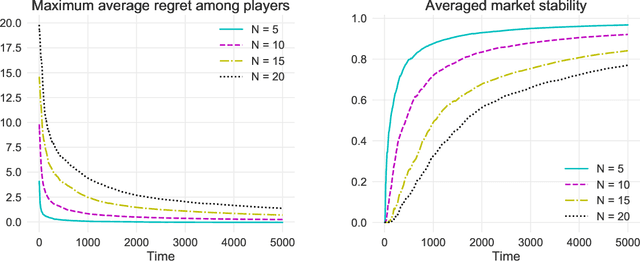
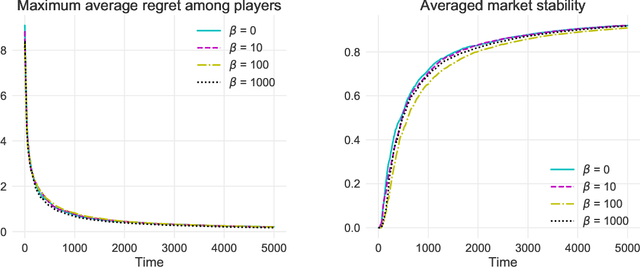
We study two-sided matching markets in which one side of the market (the players) does not have a priori knowledge about its preferences for the other side (the arms) and is required to learn its preferences from experience. Also, we assume the players have no direct means of communication. This model extends the standard stochastic multi-armed bandit framework to a decentralized multiple player setting with competition. We introduce a new algorithm for this setting that, over a time horizon $T$, attains $\mathcal{O}(\log(T))$ stable regret when preferences of the arms over players are shared, and $\mathcal{O}(\log(T)^2)$ regret when there are no assumptions on the preferences on either side.

Balancing Competing Objectives with Noisy Data: Score-Based Classifiers for Welfare-Aware Machine Learning

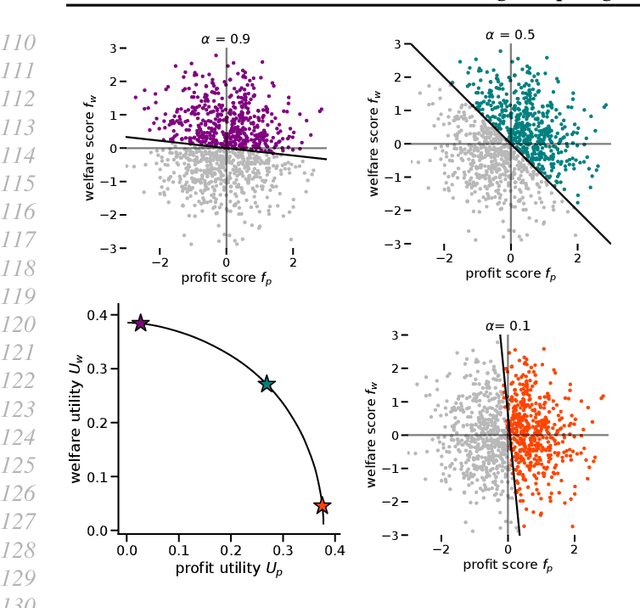
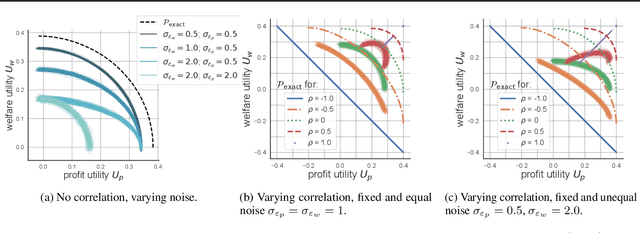
While real-world decisions involve many competing objectives, algorithmic decisions are often evaluated with a single objective function. In this paper, we study algorithmic policies which explicitly trade off between a private objective (such as profit) and a public objective (such as social welfare). We analyze a natural class of policies which trace an empirical Pareto frontier based on learned scores, and focus on how such decisions can be made in noisy or data-limited regimes. Our theoretical results characterize the optimal strategies in this class, bound the Pareto errors due to inaccuracies in the scores, and show an equivalence between optimal strategies and a rich class of fairness-constrained profit-maximizing policies. We then present empirical results in two different contexts --- online content recommendation and sustainable abalone fisheries --- to underscore the applicability of our approach to a wide range of practical decisions. Taken together, these results shed light on inherent trade-offs in using machine learning for decisions that impact social welfare.

Competing Bandits in Matching Markets

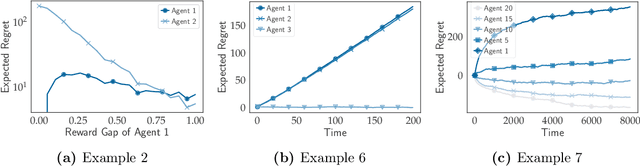
Stable matching, a classical model for two-sided markets, has long been studied with little consideration for how each side's preferences are learned. With the advent of massive online markets powered by data-driven matching platforms, it has become necessary to better understand the interplay between learning and market objectives. We propose a statistical learning model in which one side of the market does not have a priori knowledge about its preferences for the other side and is required to learn these from stochastic rewards. Our model extends the standard multi-armed bandits framework to multiple players, with the added feature that arms have preferences over players. We study both centralized and decentralized approaches to this problem and show surprising exploration-exploitation trade-offs compared to the single player multi-armed bandits setting.

Steerable $e$PCA

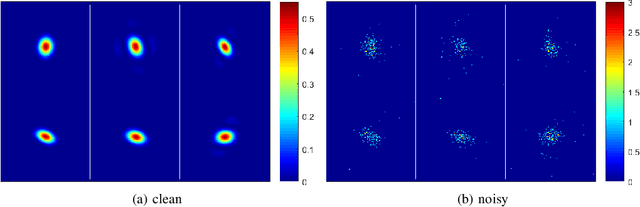
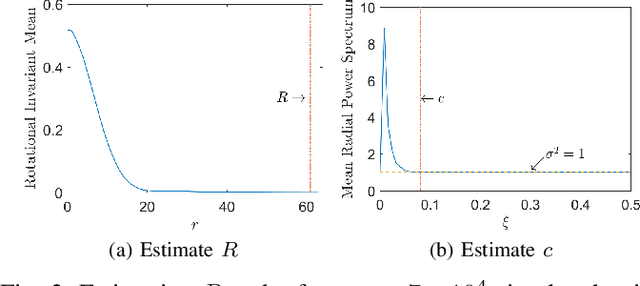
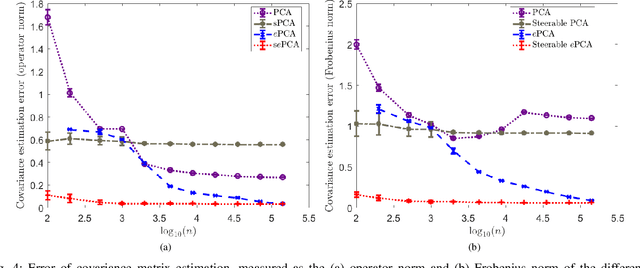
In photon-limited imaging, the pixel intensities are affected by photon count noise. Many applications, such as 3-D reconstruction using correlation analysis in X-ray free electron laser (XFEL) single molecule imaging, require an accurate estimation of the covariance of the underlying 2-D clean images. Accurate estimation of the covariance from low-photon count images must take into account that pixel intensities are Poisson distributed, rendering the sub-optimality of the classical sample covariance estimator. Moreover, in single molecule imaging, including in-plane rotated copies of all images could further improve the accuracy of covariance estimation. In this paper we introduce an efficient and accurate algorithm for covariance matrix estimation of count noise 2-D images, including their uniform planar rotations and possibly reflection. Our procedure, {\em steerable $e$PCA}, combines in a novel way two recently introduced innovations. The first is a methodology for principal component analysis (PCA) for Poisson distributions, and more generally, exponential family distributions, called $e$PCA. The second is steerable PCA, a fast and accurate procedure for including all planar rotations for PCA. The resulting principal components are invariant to the rotation and reflection of the input images. We demonstrate the efficiency and accuracy of steerable $e$PCA in numerical experiments involving simulated XFEL datasets.

On the Local Minima of the Empirical Risk

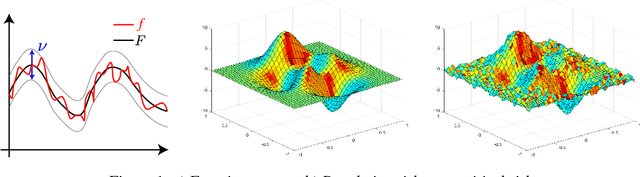
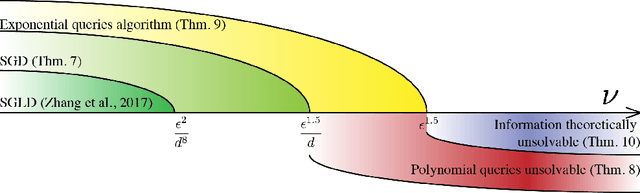
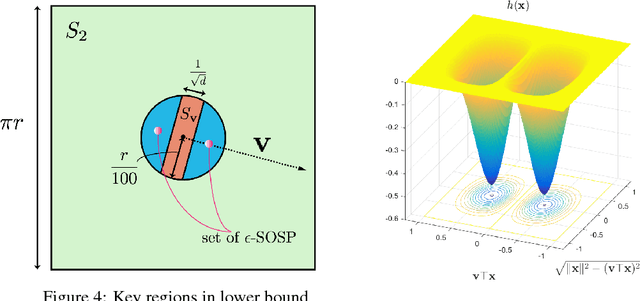
Population risk is always of primary interest in machine learning; however, learning algorithms only have access to the empirical risk. Even for applications with nonconvex nonsmooth losses (such as modern deep networks), the population risk is generally significantly more well-behaved from an optimization point of view than the empirical risk. In particular, sampling can create many spurious local minima. We consider a general framework which aims to optimize a smooth nonconvex function $F$ (population risk) given only access to an approximation $f$ (empirical risk) that is pointwise close to $F$ (i.e., $\|F-f\|_{\infty} \le \nu$). Our objective is to find the $\epsilon$-approximate local minima of the underlying function $F$ while avoiding the shallow local minima---arising because of the tolerance $\nu$---which exist only in $f$. We propose a simple algorithm based on stochastic gradient descent (SGD) on a smoothed version of $f$ that is guaranteed to achieve our goal as long as $\nu \le O(\epsilon^{1.5}/d)$. We also provide an almost matching lower bound showing that our algorithm achieves optimal error tolerance $\nu$ among all algorithms making a polynomial number of queries of $f$. As a concrete example, we show that our results can be directly used to give sample complexities for learning a ReLU unit.

Group calibration is a byproduct of unconstrained learning

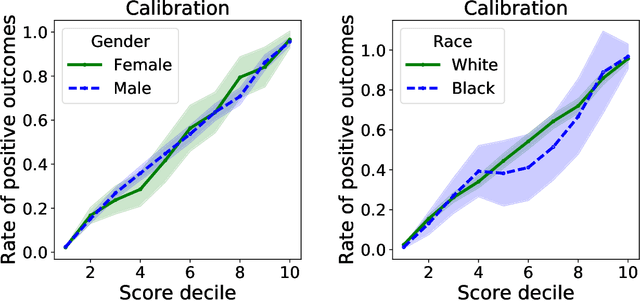
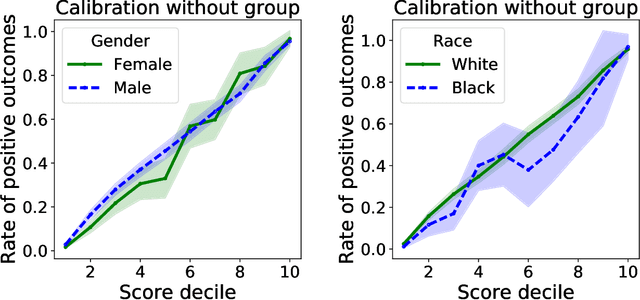
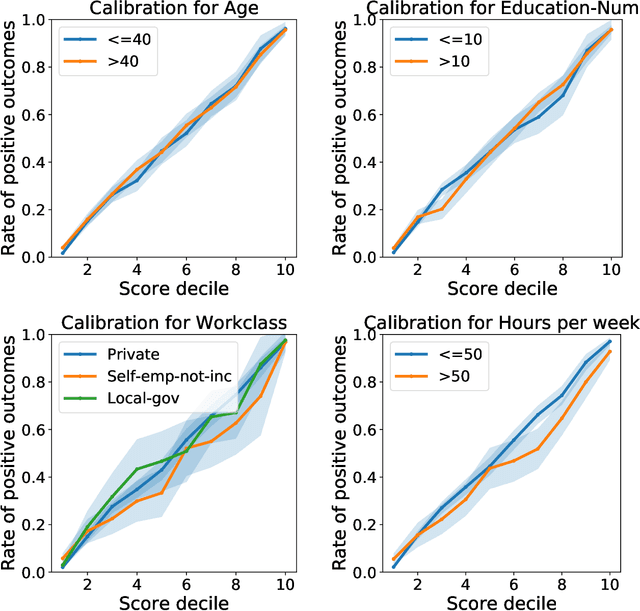
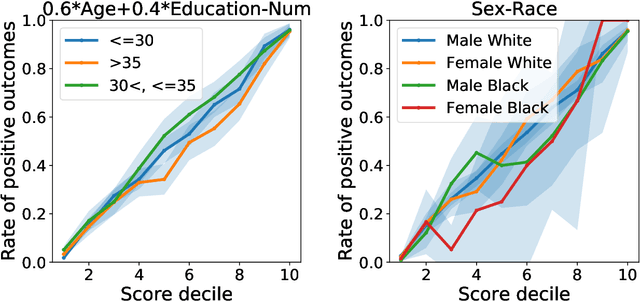
Much recent work on fairness in machine learning has focused on how well a score function is calibrated in different groups within a given population, where each group is defined by restricting one or more sensitive attributes. We investigate to which extent group calibration follows from unconstrained empirical risk minimization on its own, without the need for any explicit intervention. We show that under reasonable conditions, the deviation from satisfying group calibration is bounded by the excess loss of the empirical risk minimizer relative to the Bayes optimal score function. As a corollary, it follows that empirical risk minimization can simultaneously achieve calibration for many groups, a task that prior work deferred to highly complex algorithms. We complement our results with a lower bound, and a range of experimental findings. Our results challenge the view that group calibration necessitates an active intervention, suggesting that often we ought to think of it as a byproduct of unconstrained machine learning.

Delayed Impact of Fair Machine Learning

Fairness in machine learning has predominantly been studied in static classification settings without concern for how decisions change the underlying population over time. Conventional wisdom suggests that fairness criteria promote the long-term well-being of those groups they aim to protect. We study how static fairness criteria interact with temporal indicators of well-being, such as long-term improvement, stagnation, and decline in a variable of interest. We demonstrate that even in a one-step feedback model, common fairness criteria in general do not promote improvement over time, and may in fact cause harm in cases where an unconstrained objective would not. We completely characterize the delayed impact of three standard criteria, contrasting the regimes in which these exhibit qualitatively different behavior. In addition, we find that a natural form of measurement error broadens the regime in which fairness criteria perform favorably. Our results highlight the importance of measurement and temporal modeling in the evaluation of fairness criteria, suggesting a range of new challenges and trade-offs.